“几种语言中0.1 + 0.2结果的无聊记录。”
浮点数的表示方式
浮点数类型的表示方式:
\[signifant \times base ^ {expont}\]因此,显然会丢失部分精度,于是就有了经典的$0.1 + 0.2 \ne 0.3$问题。
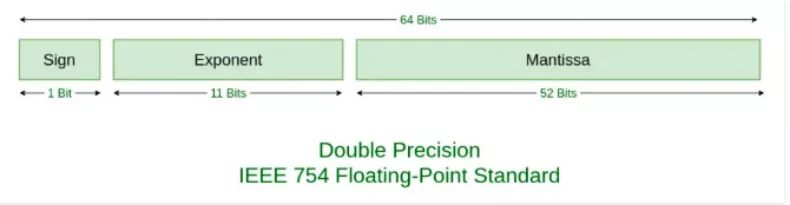
IEEE754 双精度标准
C
C语言的double类型是双精度浮点数,运算结果较为well-known:
#include <stdio.h>
int main()
{
double x = 0.1;
double y = 0.2;
double z = 0.3;
// 5.5511151231e-17
printf("%.10e", x + y - z);
return 0;
};
JavaScript
JavaScript中的所有类型都是双精度浮点数:
// 5.551115123125783e-17
console.log(0.1 + 0.2 - 0.3)
Java
Java中的字面值常量是双精度浮点数:
public class Main2 {
public static void main(String[] args) {
// 5.551115123125783E-17
System.out.println(0.1 + 0.2 - 0.3);
}
}
Haskell
-- 5.551115123125783e-17
main :: IO ()
main = print $ 0.1 + 0.2 - 0.3
Python
python中可以用decimal实现小数的准确计算
import decimal
a = decimal.Decimal('0.1')
b = decimal.Decimal('0.2')
c = decimal.Decimal('0.3')
# 0.0
print(a + b - c)
# 5.55111512313e-17
print(0.1 + 0.2 - 0.3)